Unlocking the Mystery: Exploring the Enigmatic SS in Statistics
Mean or average calculation
In statistics, SS refers to the sum of squares, which is a calculation used to measure the variability or dispersion of a data series. It is often used in regression analysis and method validation experiments. The sum of squares can be calculated for different types of data, such as population variance or sample variance. It is a useful tool for understanding the differences between data points and can help in making comparisons or identifying patterns. By calculating the sum of squares, statisticians can determine the standard deviation, which is a measure of how spread out the data is.
This information is valuable for investors, researchers, and anyone analyzing data sets.
Understanding the sum of squares
The sum of squares (SS) is a statistical measure used to analyze the variability within a data set. It represents the sum of the squared differences between each data point and the mean.
To calculate the sum of squares, you subtract the mean from each data point, square the result, and then sum up all the squared differences.
The SS is used in various statistical techniques, such as regression analysis, to assess the goodness of fit and the variability of the data.
Understanding the concept of SS is crucial for performing method validation experiments, analyzing population variances, and assessing the quality control of a process.
By calculating the SS, you can gain insights into the variability and differences in a data series, which can be useful for making informed decisions and identifying patterns or trends.
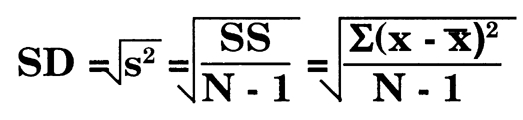
Calculation of the standard error of the mean
The standard error of the mean (SEM) is a measure of the variability of the sample mean from multiple samples. It quantifies the precision of the sample mean estimate and indicates how close the sample mean is to the true population mean.
To calculate the SEM, you need the sample standard deviation (SD) and the sample size. The formula is SEM = SD / √n, where SD is the standard deviation and n is the sample size.
For example, if you have a sample of 50 data points and the sample standard deviation is 5, the SEM would be 5 / √50 = 0.71. This means that the sample mean is estimated to be within 0.71 units of the true population mean.
Understanding the SEM is essential in statistical analysis as it helps determine the reliability of the sample mean and the precision of any inferences made from it.
Limitations of using the sum of squares
The sum of squares (SS) is a commonly used statistical measure, but it does have its limitations. One major limitation is that it only considers the squared differences from the mean, ignoring the direction of the deviation. This can lead to misleading interpretations, especially when comparing different samples or populations.
Another limitation is that SS is sensitive to extreme values, or outliers, in the data. These outliers can have a disproportionate impact on the overall SS, skewing the results. It’s important to be aware of this when analyzing data.
Additionally, SS does not provide any information about the individual data points or their distribution. It only gives a measure of the overall variability in the data.
To overcome these limitations, other statistical measures such as standard deviation, variance, or standard error can be used. These measures provide a more comprehensive understanding of the data and can be more informative in certain situations.
Resolving access issues on statisticshowto.com
If you’re experiencing access issues on statisticshowto. com, there are a few steps you can take to resolve them. First, make sure you have a stable internet connection and try clearing your browser’s cache and cookies. If the problem persists, it may be due to security measures implemented on the website.
statisticshowto. com uses Cloudflare as a security service, which can sometimes block certain actions or functions. If you believe you’ve been blocked in error, you can contact the site owner or Cloudflare directly for assistance.
Importance of the standard error and sampling distribution
The standard error and sampling distribution are important concepts in statistics. Standard error measures the variability or dispersion of sample means from the population mean. It is a crucial tool for estimating population parameters and making inferences about the population. Sampling distribution refers to the distribution of sample statistics, such as means or proportions, from repeated random sampling from a population.
It helps in understanding the variability of sample statistics and making accurate predictions about the population. Understanding these concepts is essential for conducting statistical analyses, interpreting results, and making informed decisions based on data.


